
article from math.com
Power of x.
(n |
Exponential / Logarithmic
Proof | Proof, Tip! |
Proof |
Trigonometric
Proof | Proof |
Proof | Proof |
Proof | Proof |
Trigonometric Result
Proof | Proof |
Proof | Proof |
Proof | Proof |
Inverse Trigonometric
Inverse Trigonometric Result
|
|
Hyperbolic
Proof | Proof |
Proof | |
Proof | Proof |
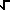 (1 - x2)
(1 - x2) /2 - arcsin x
/2 - arcsin x
Tidak ada komentar:
Posting Komentar